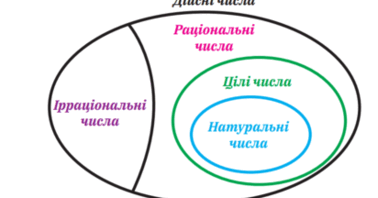
Ірраціональні числа – це тема, яка здається складною на перший погляд. Проте, якщо розібратись, вона дуже цікава й зрозуміла. У цій статті ми детально розглянемо, що таке ірраціональні числа, де вони зустрічаються, чим відрізняються від раціональних, та як легко їх впізнати.
Що таке ірраціональні числа?
Ірраціональні числа – це такі числа, які не можна представити у вигляді дробу, тобто частки двох цілих чисел. Наприклад, число π (пі) або √2 (корінь з двох) не можна записати як звичайний дріб.
Як зрозуміти ірраціональні числа простими словами?

Щоб легше зрозуміти, пригадаймо, що раціональні числа – це ті, які можна записати як a/b, де a і b – цілі числа, а b ≠ 0. Наприклад, 1/2, 3/4, або навіть 5 (бо 5 = 5/1).
Ірраціональні числа – це зовсім інші. Їх неможливо представити як дріб. Їх десятковий запис нескінченний і не має закономірності. Наприклад:
- √2 = 1.414213562…
- π = 3.141592653…
Ці числа не повторюються і не закінчуються. Саме тому вони називаються ірраціональними, тобто “нерозумними” або “не логічно поділеними”.
Приклади ірраціональних чисел
Навести приклади дуже просто, бо їх насправді багато. Ось деякі з найвідоміших:
- π (пі) – використовується в математиці та геометрії.
- e (число Ейлера) – важливе у вищій математиці.
- √2, √3, √5, √7 – корені з чисел, які не є квадратами.
- Золотий перетин (φ ≈ 1.618…) – використовується в мистецтві та архітектурі.
Як відрізнити ірраціональне число?
Це завдання, насправді, не таке складне. Ірраціональні числа:
- Не мають кінця в десятковому записі.
- Не мають періоду (повторюваних цифр).
- Не можна записати як дріб.
Якщо ви бачите √3 або π – це точно ірраціональне число.
Ірраціональні числа проти раціональних
Щоб краще розуміти тему, варто порівняти ірраціональні та раціональні числа:
| Ознака | Раціональні | Ірраціональні |
| Можна записати як дріб | Так | Ні |
| Десятковий запис | Має кінець або період | Нескінченний, без періоду |
| Приклади | 1/2, 4, -3 | π, √2, e |
Це порівняння допомагає побачити різницю дуже чітко.
Чому існують ірраціональні числа?
Це логічне запитання. Ірраціональні числа існують, бо деякі довжини або відстані не можна точно описати через звичайні дроби. Наприклад, якщо ви малюєте квадрат зі стороною 1, то діагональ буде √2, і це не можна представити як раціональне число.
Хто відкрив ірраціональні числа?
Історія говорить, що ще давньогрецькі математики, зокрема піфагорійці, першими зіткнулись з ірраціональними числами. Вони були шоковані, коли дізнались, що √2 – це не раціональне число. Спочатку це навіть тримали у таємниці!
Де використовують ірраціональні числа?
Ірраціональні числа трапляються частіше, ніж ви думаєте:
- У геометрії – довжина діагоналі квадрата, коло тощо.
- У фізиці – розрахунки хвиль, швидкостей, енергії.
- У будівництві – при проєктуванні пропорцій.
- У програмуванні – для точних обчислень.
Отже, навіть у звичайному житті вони дуже важливі.
Чому важливо знати про ірраціональні числа?
Вивчення ірраціональних чисел допомагає:
- Краще розуміти математику.
- Готуватися до ЗНО або контрольних робіт.
- Розвивати логіку та мислення.
Знання про ці числа розширює кругозір і дає глибше розуміння природи чисел.
Які числа не є ірраціональними?
Дуже важливо не плутати. Якщо число можна представити як дріб, навіть нескінченний періодичний десятковий запис, – це не ірраціональне число.
Наприклад:
- 0.3333… = 1/3 – це раціональне число.
- 1.27272727… = 14/11 – також раціональне.
Цікаві факти про ірраціональні числа
- π – одне з найвідоміших чисел у світі, має окремий день – 14 березня (День Пі).
- √2 – ще називають першим відкритим ірраціональним числом.
- Число е є основою логарифмів.
Ірраціональні числа на координатній прямій
На числовій прямій ірраціональні числа займають всі проміжки, де немає раціональних чисел. Тобто між будь-якими двома раціональними числами завжди є ірраціональні. Це показує, наскільки вони поширені.
Як працювати з ірраціональними числами?
Хоча ці числа не мають точного значення, з ними можна:
- Округлювати до потрібної кількості знаків.
- Використовувати в формулах.
- Розраховувати площі, довжини, об’єми.
Важливо знати, як ними користуватись навіть без точної величини.
Чому π – ірраціональне число?
Число π – це відношення довжини кола до його діаметра. Це відношення не має кінця і не повторюється. Через це воно ірраціональне. Його значення – 3.14159265… і так далі без кінця.
Читати далі: Теорема синусів – Повний гід для учнів та студентів
Часті запитання про ірраціональні числа
Ірраціональні числа – це числа, які не можна подати у вигляді дробу, і їх десятковий запис нескінченний без повторення.
√2, π, e – найпоширеніші приклади ірраціональних чисел.
Ірраціональні числа не можна подати як дріб, а раціональні – можна.
У математиці, фізиці, будівництві, архітектурі, та навіть у мистецтві.
Так, в реальних обчисленнях ірраціональні числа зазвичай округлюють до зручної кількості знаків після коми.
Висновок: чому варто вивчати ірраціональні числа?
Отже, ірраціональні числа – це незвичайні, але дуже важливі числа в математиці. Вони не мають точного дробового представлення, але їх значення можна обчислювати та використовувати. Завдяки ним ми можемо точніше описувати світ, розраховувати об’єми, довжини, кути й навіть розуміти природні пропорції.
Навіть якщо вам здається, що це складно – не хвилюйтесь. Якщо читати поступово й з прикладами, як у цій статті, тема стає дуже зрозумілою. Адже математика – це не страшно, якщо пояснити просто.