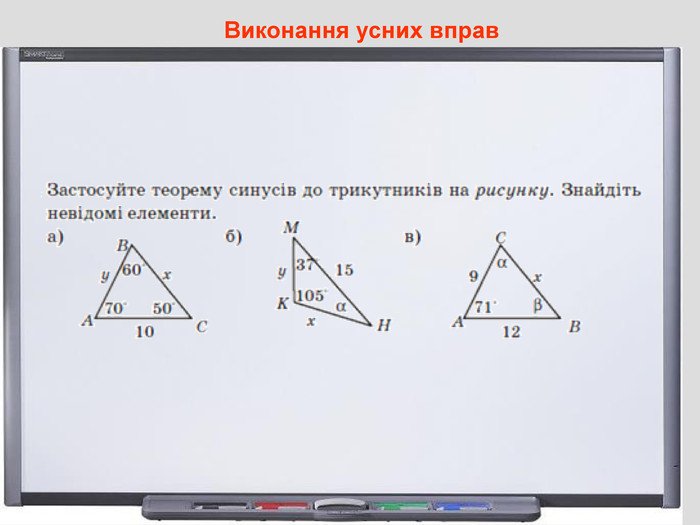
Теорема синусів - Повний гід для учнів та студентів

Теорема синусів — це один із найважливіших законів у геометрії, який допомагає працювати з трикутниками. Вона з’єднує сторони і кути трикутника у просту й елегантну формулу, що значно полегшує розв’язання задач. Далі ми детально розглянемо, що таке теорема синусів, як її використовувати, приклади застосування та корисні поради.

Contents

Теорема синусів: Основне визначення

Теорема синусів стверджує, що у будь-якому трикутнику відношення довжини сторони до синуса протилежного кута є однаковим для всіх трьох сторін. Інакше кажучи, формула виглядає так:

asin⁡A=bsin⁡B=csin⁡C\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}sinAa=sinBb=sinCc

де aaa, bbb, ccc — сторони трикутника, а AAA, BBB, CCC — відповідні кути. Таким чином, навіть у складних ситуаціях, знаючи декілька елементів трикутника, можна знайти невідомі величини.

Теорема синусів: Історія та відкриття

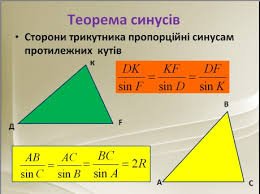
Цікаво, що теорема синусів має глибоке коріння в історії математики. Вона була відома ще стародавнім грекам. Наприклад, астроном Гіпарх першим використав ідеї, що наближалися до сучасної формулювання теореми синусів. Однак повноцінна форма з’явилася в працях мусульманських математиків середньовіччя, які займалися розвитком тригонометрії. Отже, теорема синусів має тисячолітню історію і є доказом важливості тригонометричних знань.

Теорема синусів: Коли її застосовують

Насамперед, теорему синусів використовують для розв’язання трикутників, де:

Відомо дві сторони і кут, що не є між ними (випадок SSA).
Відомо дві кути і одну сторону (випадок AAS або ASA).
Потрібно знайти площу трикутника, використовуючи сторони і кути.

Теорема синусів дозволяє обчислювати невідомі елементи без складних обчислень або креслень. Це особливо корисно в геодезії, астрономії та фізиці.

Теорема синусів: Покрокове застосування

Щоб правильно скористатися теоремою синусів, потрібно дотримуватися кількох простих кроків:

Запишіть відому інформацію: сторони і кути трикутника.
Визначте, яку сторону або кут потрібно знайти.
Підставте відомі значення у формулу.
Використовуйте пропорцію для обчислення невідомого елемента.

Цей процес, як правило, дуже прямолінійний, що робить теорему синусів неймовірно зручною навіть для новачків.

Теорема синусівв: Приклад розв’язання задачі

Розглянемо простий приклад. Нехай у трикутнику відомо:

Сторона a=7a = 7a=7 см,
Кут A=45∘A = 45^\circA=45∘,
Кут B=60∘B = 60^\circB=60∘.

Потрібно знайти сторону bbb.

Використовуємо теорему синусів:

asin⁡A=bsin⁡B\frac{a}{\sin A} = \frac{b}{\sin B}sinAa=sinBb

Підставляємо дані:

7sin⁡45∘=bsin⁡60∘\frac{7}{\sin 45^\circ} = \frac{b}{\sin 60^\circ}sin45∘7=sin60∘b

Обчислюємо значення синусів:

sin⁡45∘=22,sin⁡60∘=32\sin 45^\circ = \frac{\sqrt{2}}{2}, \quad \sin 60^\circ = \frac{\sqrt{3}}{2}sin45∘=22,sin60∘=23

Підставляємо:

722=b32\frac{7}{\frac{\sqrt{2}}{2}} = \frac{b}{\frac{\sqrt{3}}{2}}227=23b

Після перетворень отримаємо:

b=7×32≈8.57 смb = 7 \times \frac{\sqrt{3}}{\sqrt{2}} \approx 8.57 \, \text{см}b=7×23≈8.57см

Отже, сторона bbb дорівнює приблизно 8.578.578.57 см.

Теорема синусівв: Типові помилки

Хоча теорема синусівв здається простою, часто допускаються типові помилки:

Неправильне визначення кутів (забувають, що сума кутів у трикутнику дорівнює 180 градусів).
Використання неправильних одиниць виміру (наприклад, радiани замість градусів).
Невірне округлення значень синусів.

Щоб уникнути таких помилок, завжди уважно перевіряйте вихідні дані та проміжні обчислення.

Теорема синусівв: У трикутниках із тупим кутом

Окремо варто звернути увагу, що теорема синусівв працює і в трикутниках з тупим кутом. Але в таких випадках потрібно бути обережним із визначенням синуса кута, особливо коли працюєте з тригонометричними таблицями або калькуляторами.

Теорема синусівв: Зв’язок із іншими теоремами

Цікаво, що теорема синусівв тісно пов’язана з теоремою косинусів. Хоча їх використовують у різних ситуаціях, обидві теореми дають змогу вирішувати трикутники. Теорема косинусів більше підходить для знаходження сторін за відомими сторонами і кутами, тоді як теорема синусівв зручніша, коли відомо більше кутів.

Теорема синусівв: Застосування в реальному житті

Теорема синусівв використовується не тільки в шкільній математиці. Вона є важливою у навігації, геодезії, інженерії та навіть у медицині. Наприклад, при створенні карт або у тріангуляції для мобільного зв’язку часто використовують саме теорему синусів.

Теорема синусівв: Чому варто вивчити

По-перше, знання теореми синусів допомагає глибше розуміти природу геометрії. По-друге, це корисна навичка для різних професій, що потребують просторового мислення. Нарешті, це відмінна тренування для мозку, яка вчить логіці, уважності та акуратності.

Читати далі: Прийменник це – Повне пояснення для школярів з прикладами